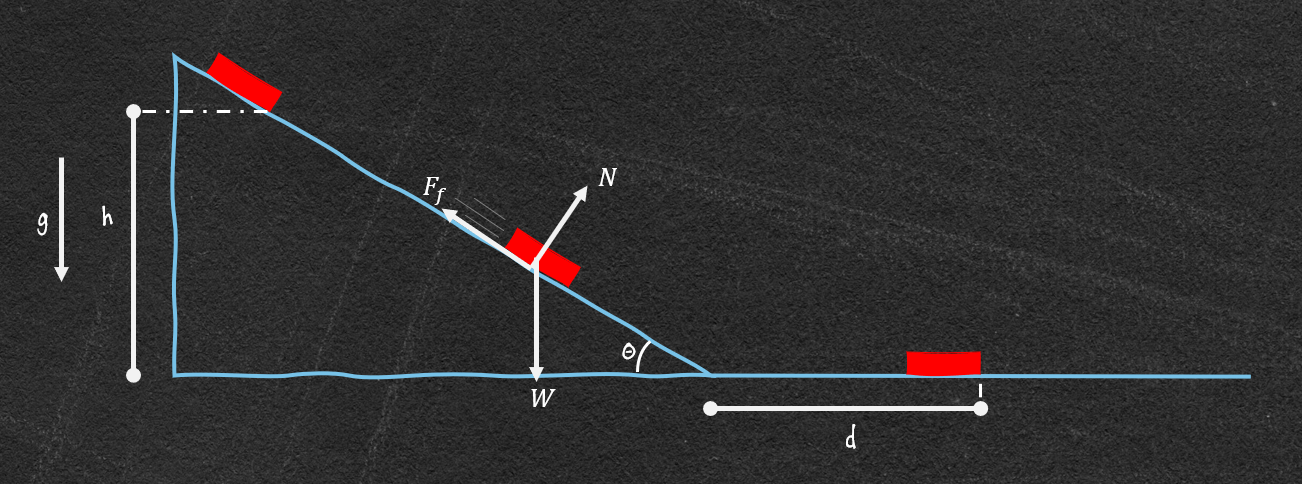
In the last post, we analyzed a sled down a snowy hill and included friction in the problem. Now, for part 2, we are going to look at how far the sled goes after it hits the level ground, in other words, solve for \(d\).

From the previous post, the acceleration of the sled going down the hill is
\(\ddot{x} = g \sin(\Theta) – \mu g \cos(\Theta)\)
And remember, here \(\ddot{x}\) is the direction of motion of the sled.
Simplifications
To continue solving this problem, we’re going to make a simplification. We are going to assume the sled when it hits the boundary between the hill and the level ground makes the transition fluidly without loss of velocity.


Now, to see how far this goes, we’ll need to create a new force diagram for the sled on the horizontal ground. From figure 4, we can see that there is only one force that really matters here. The force of (kinetic) friction is slowing the sled down.
Hitting A Snag

We can now write down the sum of the forces in the X direction
\(\sum F_{x} = m \ddot{x} = -\mu N\)
And this reduces to
\(\ddot{x} = -\mu g\)
Now we know the acceleration, but this puts us in a bit of a quandary because we only know the acceleration, and that is not enough information to find out the distance. Ultimately, we also need to know the velocity and time.
Sled Velocity
So, we know we need to know the velocity of the sled when it levels out, and this is where our simplification from above comes in. Where we assume there is no loss of momentum from the hill to the level ground. Using that simplification and a few equations, we should be able to solve this problem. The equations are:
\(v_f – v_0 = a t\)
Starting with the one on the left, we know the sled starts at rest and sleds down the hill, which gives us
\(v_f – 0 = a t \Rightarrow \frac{v_f}{a} = t\)
Plugging this into the \(x(t)\) gives us
\(x_f = x_0+ \frac{v_f^{2}}{2 a}\)
And this can be rearranged to
\(x_f – x_0 = \frac{v_f^{2}}{2 a}\)
Now what are \(x_f\) and \(x_0\)? We will need to define a zero, an origin, and let’s define it as in figure 5. Sidenote: This may seem a little convoluted, perhaps backward, or like a different origin makes more sense. That’s not a poor argument, I chose this one so I wouldn’t have to move it later and to illustrate negative distance.

Because of where we have the origin, this means \(x_f = 0\). To figure out \(x_0\), we’ll need to know the height the sled starts, the angle of the hill, and some simple trigonometry. It’s a right triangle so we know
\(sin(\Theta)=\frac{h}{x} \Rightarrow \frac{h}{sin(\Theta)}=x \)
This x is equal to \(x_0\), but it’s not just \(x_0\) it is \(-x_0\) because of where the origin is. Plugging it all in gives us
\(0 – (-\frac{h}{sin(\Theta)}) = \frac{v_f^{2}}{2 a}\)
Rearranging gives us
\(v_f^{2} = \frac{2 \space a \space h}{sin(\Theta)}\)
The acceleration for this would be the acceleration we figured out in part 1
\(v_f^{2} = \frac{2 h (g \sin(\Theta) – \mu \space g \cos(\Theta))}{sin(\Theta)}\)
Now For The Distance
This \(v_f\) will be the initial velocity for the sled on the horizontal ground, and we can use the same \(x_f\) and \(v_f-v_0\) equations above.
\(v_f – v_0 = a \space t\)
\(0 – v_0 = -\mu \space g \space t\)
\(t = \frac{v_0}{\mu \space g}\)
\(x_f = x_0+v_0 t + \frac{1}{2} a \space t^{2}\)
\(d = 0+v_0 t + \frac{1}{2} (-\mu \space g) t^{2}\)
\(d = \frac{v_0^{2}}{\mu \space g} + \frac{1}{2} (-\mu \space g) (\frac{v_0}{\mu \space g})^{2}\)
\(d = \frac{v_0^{2}}{2 \space \mu \space g}\)
Great! Now we know \(d\) and all of the other variables, putting it all together
\(d = \frac{2 h (g \sin(\Theta) – \mu \space g \space \cos(\Theta))}{ 2 \mu \space g \space sin(\Theta)}\)
\(d = h (\frac{\sin(\Theta)}{\mu} – \cot(\Theta))\)
Sanity Check
Like in part 1, we need to check that this solution makes sense with some limit checks.
\(\mu \rightarrow 0 \Rightarrow d \rightarrow \infty\) And this makes sense because without friction the sled would never stop.
It’s important to notice that trying to modify \(\Theta\) without \(h\) will give the wrong limits because they are simultaneously changing limits. Let’s transform the equation back to \(x\) from \(h\)
\(d = x \sin(\Theta) (\frac{\sin(\Theta)}{\mu} – \cot(\Theta))\)
\(d = x (\frac{\sin^2(\Theta)}{\mu} – \cos(\Theta))\)
Now, taking the limit as \(\Theta \rightarrow 0\), we get
\(d = -x\)
No motion, no nothing, just a position.
What if?
What if the coefficients of friction were different between the hill and the horizontal plane? What if there was no horizontal and instead it was another hill causing the sled to go uphill, how high would the sled go?